TURUNAN

ini bentuk limit alternatif dari turunan yang berguna untuk menyelidiki hubungan antara turunan dan kekontinuan. Turunan f di c adalah

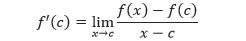
apabila limitnya ada. Perhatikan gambar berikut.

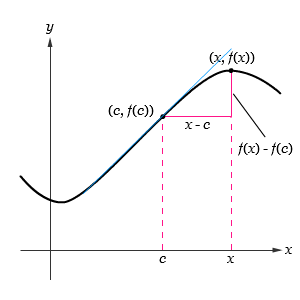
Yang perlu diperhatikan adalah bahwa nilai limit pada bentuk alternatif ini dikatakan ada apabila

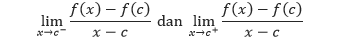
ada dan sama. Limit seperti ini secara berturut-turut disebut turunan dari kiri dan dari kanan. Dari uraian tersebut kita dapat mengatakan bahwa f memiliki turunan pada selang tutup [a, b] jika f memiliki turunan pada (a, b) dan jika turunan dari kanan a dan turunan dari kiri b, kedua-duanya ada.
Jika suatu fungsi tidak kontinu pada x = c, maka fungsi tersebut juga tidak akan memiliki turunan di x = c. Sebagai contoh, fungsi bilangan bulat terbesar

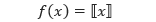
tidak kontinu di x = 0, yang menyebabkan tidak akan memiliki turunan di x = 0. Perhatikan gambar di bawah.

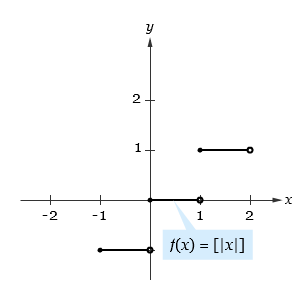
Kita dapat membuktikan bahwa f tersebut tidak memiliki turunan di x = 0, sebagai berikut.

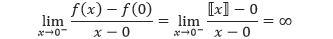
dan

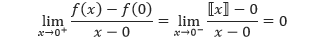
Walaupun benar bahwa turunan mengakibatkan kekontinuan, akan tetapi konvers dari pernyataan ini belum tentu benar. Dengan kata lain, ada kemungkinan suatu fungsi kontinu di x = c, tetapi tidak memiliki turunan di x = c. Contoh 1 dan 2 berikut mengilustrasikan kemungkinan tersebut.
Contoh 1: Grafik dengan Belokan Tajam
Fungsi f(x) = |x – 1| seperti yang ditunjukkan oleh gambar di bawah, merupakan fungsi yang kontinu di x = 1. Akan tetapi,

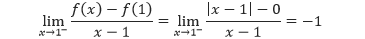
dan

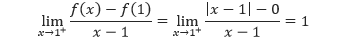
tidak sama. Sehingga f tidak memiliki turunan di x = 1 dan grafiknya tidak memiliki garis singgung di titik (1, 0).

Contoh 2: Grafik dengan Garis Singgung Vertikal
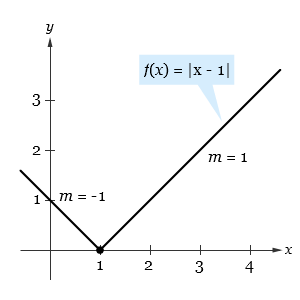
Fungsi f(x) = x^1/3 kontinu pada x = 0, seperti yang ditunjukkan oleh gambar di bawah ini.

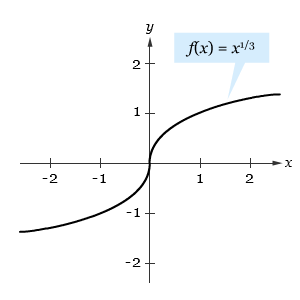
Akan tetapi karena limit

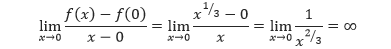
tak terhingga, kita dapat menyimpulkan bahwa garis singgungnya vertikal ketika x = 0. Sehingga, f tidak memiliki turunan pada x = 0.
Dari contoh 1 dan 2, kita dapat melihat bahwa suatu fungsi tidak memiliki turunan pada suatu titik ketika grafiknya belok tajam dan garis singgungnya vertikal.

Teorema: Turunan Menyebabkan Kekontinuan
Jika f memiliki turunan pada x = c, maka f kontinu pada x = c.

Bukti: Kita dapat membuktikan bahwa f kontinu pada x = c dengan menunjukkan bahwa f(x) mendekati f(c) ketika x → c. Untuk menunjukkan ini, kita gunakan turunan pada x = c dan menentukan limit berikut.

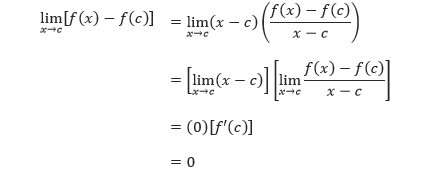
Karena selisih f(x) – f(c) mendekati 0 ketika x → 0, kita dapat menyimpulkan bahwa limit f(x) dengan x → c sama dengan f(c). Sehingga, f kontinu pada x = c.

Tugas  dan  wewenang MPR

1.   Mengubah dan menetapkan  UUD

2.  Melantik presiden dan wakil presiden berdasarkan hasil pemilihan umum dalam sidang paripurna MPR

3.  Memutuskan usul DPR berdasarkan putusan mahkamah konstitusi untuk memberhentikan presiden dan atau wakil presiden dalam masa jabatannya setelah presiden dan atau wakil presiden diberi kesempatan untuk menyampaikan penjelasan di dalam sidang paripurna MPR.

4. Melantik wakil peresiden menjadi presiden apabila presiden mangkat, berhenti, diberhentikan atau tidak dapat melaksanakan kewajibannya dalam masa jabatannya.

5.  Memilih wakil presiden dari dua calon yang diajukan presiden apabila terjadi kekosongan jabatan wakil presiden dalam masa jabatannya, selambat-lambatnya dalam waktu 60 hari.

Tugas dan wewenang DPR

1.   Membentuk UU yang dibahas dengan presiden untuk mendapat persetujuan bersama;

2.     Membahas dan memberikan persetujuan peraturan pemerintah pengganti UU;

3.     Menerima dan membahas usulan rancangan UU yang diajukan DPD;

4.     Memperhatikan pertimbangan DPD atas rancangan UU anggaran pendapatan belanja Negara (APBN) dan rancangan UU yang berkaitan dengan pajak, pendidikan dan agama;

5.      Menetapkan APBN brsama presiden dengan memperhatikan pertimbangan DPD.

Tugas dan wewenang DPD

1.   Engajukan kepada DPR tentang rancangan UU yang berkaitan dengan otonomi daerah, hubungan pusat dan daerah, pembentukan dan pemekaran, penggabungan daerah, pengelolaan sumber daya alam dan sumber daya ekonomi.

2.  Membahas rancangan UU yang berkaitan dengan pelaksanaan otonomi daerah, hubungan pusat dan daerah pembentukan, pemekaran dan penggabungan daerah pengelola sumber daya alam dan sumberdaya ekonomi lainnya serta yang berkaitan dengan perimbangan keuangan pusat dan daerah yang diajukan, baik oleh DPR maupun oleh pemerintah.

3.  Memberikan pertimbangan kepada DPR atas rancangan UU APBN dan rancangan UU yang berkaitan dengan pajak, pendidikan, dan agama. 

4. Melakukan pengawasan atas pelaksanaan UU mengenai otonomi daerah, pembentukan pemekaran, dan penggabungan daerah, hubungan pusat dan daerah, pengelola sumber daya alam, dan sumber daya ekonomi laiinya, pelaksanaan APBN, pajak, pendidikan dan agama.

Pengertian Tari

Tari adalah desakan perasaan manusia di dalam dirinya yang mendorongnya untuk mencari ungkapan yang berupa gerak-gerak yang ritmis.

Sedangkan Corrie Hartong, ahli tari dari Belanda, mengajukan batasan tari yang berbunyi tari adalah gerak-gerak yang diberi bentuk dan ritmis dari badan didalam ruang.

Tari adalah gerakan tubuh sesuai dengan irama yang mengiringinya.

Tari adalah ungkapan jiwa manusia melalui gerak ritmis sehingga dapat menimbulkan daya pesona. Yang dimaksud ungkapan jiwa adalah meliputi cetusan rasa dan emosional yang disertai kehendak.

Menurut Dr Soedarsono, pakar tari Indonesia terkemuka, tari adalah ekspresi jiwa manusia melalui gerak-gerak ritmis yang indah.

Dasar pada semua definisi tari

adalah konsep ritmis dan pola gerak. Sesungguhnya pengertian tersebut tidak cukup untuk mengenali tari, begitu banyak gerak ritmis yang dilakukan manusia.

Tari adalah ekspresi dari jiwa manusia yang dilakukan melalui gerak berirama dan indah.

Definisi Seni Tari

Seni tari adalah ungkapan jiwa yang disalurkan/diek- presikan melalui gerak-gerak organ tubuh yang ritmis, indah mengandung kesusilaan dan selaras dengan gending sebagai iringan.

Seni Tari adalah ungkapan seni yang mempergunakan tubuh sebagai media alat gerak. Gerakan dalam tari untuk mencapai suatu kandungan yang terarah, harus dilandasi oleh penghayatan yang mendalam, kreatif.

Seorang ahli tari dari jawa pangeran suryadiningrat memberi definisi seni tari adalah sebagai gerak dari seluruh anggota tubuh manusia yang disusun selaras dengan irama musik serta mempunyai maksud tertentu.

Conditional Sentence Type I

Conditional Sentence Type I

Kalimat conditional disebut juga dengan kalimat pengandaian. Perhatikan contoh di bawah ini:

If I have a lot of money, I will go to America.

I will sleep if I am sleepy.

If my father has much money, he will buy a new house.

Ketiga contoh di atas adalah contoh dari conditional sentence. Conditional sentence terdiri dari 2 bagian yaitu: subordinate clause dan main clause. Subordinate clause (if + clause) merupakan pernyataan syarat atau kondisi. Sedangkan main clause pada conditional sentence adalah pernyataan akibat terpenuhinya (+) atau tidak terpenuhinya (-) persyaratan yang ada pada subordinate clause atau kondisi yang ada pada subordinate clause.

Perhatikan kembali contoh di atas:

If  I have a lot of money…(subordinate clause) kalimat ini merupakan syarat untuk terjadinya sesuatu yaitu : I will go to America. (main clause). Jadi saya akan pergi ke Amerika jika saya mempunyai banyak uang.

Semoga dengan penjelasan 1 contoh ini anda bisa memahami apa itu conditional sentence. Conditional sentence mempunyai 3 macam bentuk atau type, yaitu type 1, 2, dan 3.

Conditional sentence type 1

Conditional sentence type 1 ini bermakna future karena akibat (main clause) berbentuk future dan subordinate clause berbentuk simple present tense.  kejadian yang ada pada main clause yang berbentuk future tersebut akan terjadi bila persyaratan yang ada pada subordinate clause (if…) terpenuhi. Kita tidak mengetahui secara pasti apakah kalimat pada main clause akan benar-benar terjadi di masa yang akan datang (future), akan tetapi kondisi yang ada pada subordinate clause sangat rasional dan realistis jadi kemungkinan besar akan terjadi. Anda bingung? Perhatikan contoh ini;

If I have much money, I will go to America.

Kalimat pada subordinate clause sangat realistis,bukan? Jika saya banyak uang… maka saya akan pergi ke Amerika. Jadi kemungkinan keinginan untuk pergi ke Amerika bisa saja terjadi jika punya banyak uang. Dan persyaratan atau alasannya sangat masuk akal.

You will not pass the exam if you do not study.

Kamu tidak akan lulus ujian jika tidak belajar…bagaimana? Masuk akal bukan?

Rumus condtional sentence type 1

If +simple present tense, Simple future tense

Simple future tense + if + simple present tense

Pembuatan kalimatnya tidaklah sulit jika anda memahami simple present tense dan juga simple future. Jika anda belum memahaminya, silahkaan baca penjelasannya pada materi dasar II dan Intermediate.

NOTE: jangan lupa memasukan , (comma) jika anda meletakkan subordinate clause terlebih dahulu. Tidak perlu meletakkan koma jika main clause anda masukan terlebih dahulu.

If she has my address, she will send the invitation to me.

They will buy a car if they have money.

My mother will go to Bali if she has a lot of money.

You will be late if you sleep late.

He will not come if you are angry with him.

Penggunaan Past Perfect Continuous Tense

Penggunaan Past Perfect Continuous Tense

Past perfect continuous tense digunakan untuk:

1. Menyatakan suatu kegiatan yang terjadi di masa lampau dan masih berlanjut sampai ada kegiatan lain yang membuat kegiatan tersebut terhenti. Perhatikan contoh di bawah ini:

  

We had been playing soccer when the accident occurred. (Kami telah sedang bermain sepak bola ketika kecelakaan itu terjadi.)

Pada contoh di atas, subject telah sedang bermain bola kaki, pada saat subject telah sedang bermain bola, ada sebuah kecelakan terjadi yang membuat si subject menghentikan aktifitasnya.

2. Digunakan untuk menyatakan kegiatan yang dilakukan pada masa lampau yang mempunyai hubungan sebab akibat (cause and effect)

Contoh:

• I was so tired. I had been revising my lessons for hours.

Pada contoh di atas, “I was tired / saya lelah” merupakan akibat dari “I had been revising my lesson/saya telah sedang merevisi pelajaran-pelajaran saya selama berjam-jam”.

Pola kalimat past perfect continuous tense

Positif               : Subject + had + been + Ving

Negative           : Subject + had + not + been + Ving

Pertanyaan       : Had + Subject + been + Ving + ?

Contoh:

I had been working when she called me.

I had not been working when she called me.

Had you been working when she called you?

She had been sleeping.

She had not been sleeping.

Had she been sleeping? Yes, she had/ No, she had not