Rumus Dasar Integral

Integral merupakan sebuah konsep penting dalam matematika yang seringkali menjadi kelemahan tidak sedikit orang. Agar dapat paham dengan integral sampai integral berkelanjutan, anda pertama harus paham integral dasarnya dulu. Pondasi dari semua integral lanjutan, misalnya saja agar dapat paham integral parsial, integral tentu, integral tak tentu, dll yang akan saya berikan penjelasannya di artikel berikutnya.

Jika diberikan suatu fungsi f dari variabel x dengan interval [a,b] maka integral tertentunya dapat ditulis seperti gambar diatas. Sedangkan kurva untuk integral tersebut dapat digambarkan sebagai berikut.

Kurva diatas dapat didefinisikan sebagai daerah yang dibatasi oleh kurva f, sumbu x, sumbu y, garis x=a dan garis x=b, dimana daerah diatas sumbu x bernilai positif dan daerah dibawah sumbu x bernilai negatif.

Integral juga biasa digunakan untuk merujuk anti turunan. Jika terdapat sebuah fungsi F yang mempunyai turunan f maka kasus seperti ini disebut integral tak tentu yang dapat dinotasikan sebagai berikut.

Jika f adalah fungsi kontinu yang terdefinisi pada sebuah interval tertutup [a,b] dan jika anti turunan F dari f diketahui maka integral tertentu dari f pada interval yang telah diketahui dapat didefinisikan sebagai.

Berikut ini beberapa rumus dasar integral

Bilangan natural

$\int e^u du= e^u + C\,$

Logaritma

$\int \log_b(x) \,dx = x \log_b(x) - \frac{x}{\ln(b)} + C = x \log_b \left(\frac{x}{e}\right) + C$

Trigonometri

$\int\sin x\,dx = -\cos x + C\,$

$\int\cos x\,dx = \sin x + C\,$

$\int\tan x\,dx = \ln |\sec x| + C\,$

$\int\cot x\,dx = \ln |\sin x| + C\,$

$\int\sec x\,dx = \ln |\sec x + \tan x| + C\,$

$\int\csc x\,dx = \ln |\csc x - \cot x| + C\,$

$\int\sec^2 x\,dx = \tan x + C\,$

$\int\csc^2 x\,dx = - \cot x + C\,$

$\int\sec x\tan x\,dx = \sec x + C\,$

$\int\csc x\cot x\,dx = -\csc x + C\,$

Dalam mencari nilai integral kita dapat menggunakan beberapa cara, diantaranya :

1. Substitusi

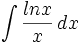
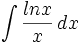
Cari nilai dari: $\int \frac{ln x}{x}\,dx\,$

$t = \ln x, dt = \frac{dx}{x}$

$\int \frac{ln x}{x}\,dx\, = \int t\,dt$

$= \frac {1}{2} t^2 + C$

$= \frac {1}{2} ln^2x + C$

2. Substitusi Trigonometri

Bentuk	Gunakan
$\sqrt{a^2-b^2x^2}\,$	$x = \frac{a}{b}\sin \alpha\,$
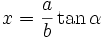$\sqrt{a^2+b^2x^2}\,$	$\!\, x = \frac{a}{b}\tan \alpha\,$
$\sqrt{b^2x^2-a^2}\,$	$\, x = \frac{a}{b}\sec \alpha\,$

Contoh soal:

Cari nilai dari: $\int \frac{dx}{x^2\sqrt{x^2+4}}\,$

$x = 2 \tan A, dx = 2 \sec^2 A\,dA\,$

$\int \frac{dx}{x^2\sqrt{x^2+4}}\,$

$= \int \frac {2 sec^2 A\,dA}{(2 tan A)^2\sqrt{4 + (2 tan A)^2}}\,$

$= \int \frac {2 sec^2 A\,dA}{4 tan^2A\sqrt{4 + 4 tan^2A}}\,$

$= \int \frac {2 sec^2 A\,dA}{4 tan^2A\sqrt{4(1+tan^2A)}}\,$

$= \int \frac {2 sec^2 A\,dA}{4 tan^2A\sqrt{4 sec^2A}}\,$

$= \int \frac {2 sec^2 A\,dA}{4 tan^2A.2sec A}\,$

$= \int \frac {sec A\,dA}{4 tan^2A}\,$

$= \frac {1}{4}\int \frac {secA\,dA}{tan^2A}\,$

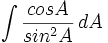$= \frac {1}{4}\int \frac{cos A}{sin^2A}\,dA\,$

Cari nilai dari: $\int \frac{cos A}{sin^2A}\,dA\,$ dengan menggunakan substitusi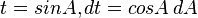

$t = sin A, dt = cos A\,dA\,$

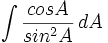
$\int \frac{cos A}{sin^2A}\,dA\,$

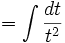
$= \int \frac{dt}{t^2}\,$

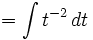
$= \int t^{-2}\,dt\,$

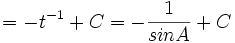
$= -t^{-1} + C= -\frac{1}{sin A} + C\,$

Masukkan nilai tersebut:

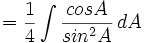
$= \frac {1}{4}\int \frac{cos A}{sin^2A}\,dA\,$

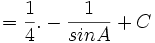
$= \frac {1}{4}.-\frac{1}{sin A} + C\,$

$= -\frac {1}{4 sin A} + C\,$

Nilai sin A adalah $\frac{x}{\sqrt{x^2+4}}$

$= -\frac {1}{4 sin A} + C\,$

$= -\frac {\sqrt{x^2+4}}{4x} + C\,$

3. Integral Parsial
Integral parsial menggunakan rumus sebagai berikut:

$\int f(x)g(x)\,dx = f'(x)g(x) - f(x)g'(x)$

Contoh soal:

Cari nilai dari: $\int \ln x \,dx\,$

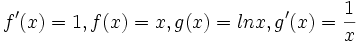
$f'(x) = 1, f(x) = x, g(x) = ln x, g'(x) = \frac{1}{x}\,$

Gunakan rumus di atas

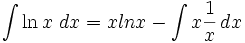
$\int \ln x\ dx = x ln x - \int x\frac{1}{x}\,dx\,$

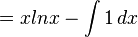
$= x ln x - \int 1\,dx\,$

$= x ln x - x + C\,$

Jika kita menemukan bentuk penjumlahan atau bentuk pengurangan integral dapat dirubah seperti berikut ini.

Nah, itulah beberapa rumus dasar integral dan contoh dalam penyelesaian integral. Semoga anda dapat memahaminya sehingga anda dapat dengan mudah memahami integral lanjutan dan berbagai jenis integral lainnya. Dari penjelasan diatas sepertinya sekarang anda telah dapat mengerjakan soal-soal integral sederhana. Maka jika anda menemukan soal-soal yang berhubungan dengan integral anda tidak akan kesulitan dalam mengerjakannya. Jangan lupa baca juga artikel sebelumnya Pengertian dan Metode Penyelesaian Persamaan Kuadrat agar anda lebih mengenal matematika dan lebih cinta matematika.

Senin, 25 November 2013

Rumus Dasar Integral

Bilangan natural

Logaritma

Trigonometri

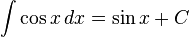
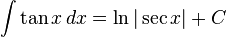
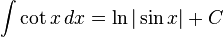
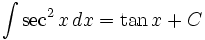
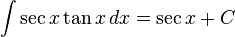
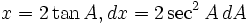
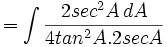
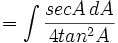
Tidak ada komentar:

Posting Komentar

PROFILE

Label

JAM

DAFTAR BLOG

MUSIC

REAL MADRID

Popular Posts

Blog Archive

Followers